位运算使用技巧

位运算概览

符号	描述	运算规则
&	与	两个位都为1时，结果才为1 【选中A标签和B标签的用户bitmap=选中A标签的用户bitmap & 选中标签的用户bitmap】
\|	或	两个位都为0时，结果才为0 【选中A或B标签的用户bitmap=选中A标签的用户bitmap
^	异或	两个位相同为0，相异为1【可用于取非数据，如不包含某个标签的用户bitmap=全量用户bitmap ^ 包含某个标签的用户bitmap】
~	取反	0变1，1变0
«	左移(每左移 1 位就乘以 2)	各二进位全部左移若干位，高位丢弃，低位补0 【2的10次方=1024】
»	右移(每右移 1 位就除以 2)	各二进位全部右移若干位，对无符号数，高位补0，有符号数，各编译器处理方法不一样，有的补符号位（算术右移），有的补0（逻辑右移）

优点

由于位运算直接对内存数据进行操作，不需要转成十进制，因此处理速度非常快。

逻辑与、逻辑或、异或的使用场景

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


/**
 * 逻辑与、逻辑或、异或的使用场景：配合数字1,2,4,8..等 2的倍数 进行使用
 * 用于数据库单个字段一个数字便包含多个信息标识，如数字7，包含数字标识：1，2，4
 */
func main() {
    // 假设有5个类别
    type1 := 1
    type2 := 2
    type3 := 4
    type4 := 8
    type5 := 16

    types := type1 | type2 | type3 | type4 | type5 // 逻辑或求并集
    fmt.Println(types) // 十进制：31，二进制：11111

    types = types ^ type4 // 逻辑异或，去掉type4
    fmt.Println(types) // 十进制：23，二进制：10111

    fmt.Println((types & type1) == type1) // true，逻辑与求交集
    fmt.Println((types & type2) == type2) // true
    fmt.Println((types & type3) == type3) // true
    fmt.Println((types & type4) == type4) // false
    fmt.Println((types & type5) == type5) // true
    fmt.Println((types& (type1+type2)) == (type1+type2)) // true
}

按位左移的使用场景

a « b 就表示把 a 转为二进制后左移 b 位（在后面添 b 个 0）。例如 100 的二进制为 1100100，而 110010000 转成十进制是 400，那么100 « 2 = 400。可以看出，a « b的值实际上就是 a 乘以 2 的 b 次方，因为在二进制数后添一个 0 就相当于该数乘以 2。

通常认为 a « 1 比 a * 2 更快，因为前者是更底层一些的操作。因此程序中乘以 2 的操作请尽量用左移一位来代替。

按位右移的使用场景

a » b 表示二进制右移 b 位（去掉末 b 位），相当于 a 除以 2 的 b 次方（取整）。我们也经常用 » 1 来代替 div 2，比如二分查找、堆的插入操作等等。

如 5»2=1，9»2=2

Bitmap

位图（Bitmap），即位（Bit）的集合，是一种数据结构，可用于记录大量的0-1状态，在很多地方都会用到，比如Linux内核（如inode，磁盘块）、Bloom Filter算法等，其优势是可以在一个非常高的空间利用率下保存大量0-1状态。

Bitmap 其本质上是采用了bit位来表示元素状态，从而在特定场景下能够极大的节省存储空间，非常适合对海量数据的查找，判重，删除等问题的处理。

原理

BitMap 从字面的意思，很多人认为是位图，其实准确的来说，翻译成基于位的映射。

BitMap 的基本原理就是用一个 bit 位来存放某种状态，适用于大规模数据，但数据状态又不是很多的情况。通常是用来判断某个数据存不存在的。

举例：在Java里面一个int类型占4个字节，假如要对于10亿个int数据进行处理呢？10亿*4/1024/1024/1024=4个G左右，需要4个G的内存。

如果能够采用bit储,10_0000_0000Bit=1_2500_0000byte=122070KB=119MB, 那么在存储空间方面可以大大节省。

我们来看看具体存储：

对于1，3，5，7这四个数，如果存在的话，则可以这样表示：

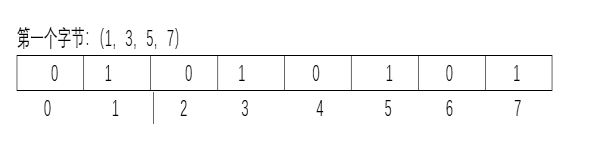
1代表这个数存在，0代表不存在。例如表中01010101代表1，3，5，7存在，0，2，4，6不存在。那如果8，10，14也存在怎么存呢？如图，8，10，14我们可以存在第二个字节里

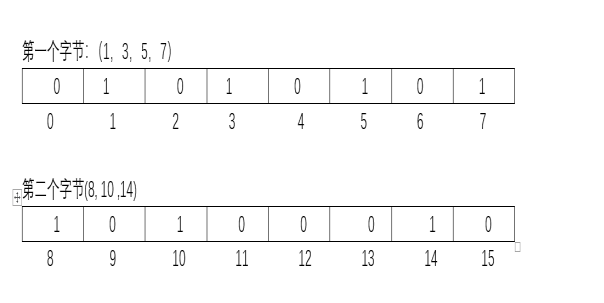
以此类推。

bitmap应用

可进行数据的快速查找，判重，删除，一般来说数据范围是int的10倍以下。
去重数据而达到压缩数据

缺点

无法进行『非运算』。

参考文章

牛逼的Bitmap算法

文章目录